
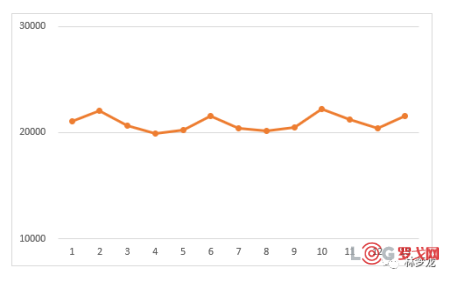
指数平滑法是一种比较常用的时间序列预测法。其原理是任一期的指数平滑值是本期实际观察值与前一期指数平滑值的加权平均,这种方法融合了新旧价值信息,赋予较新信息更大的权重。
这样做的重要意义是,因为预测上,越接近现在的信息越比较可信,而越远的信息,历史陈旧则可信程度没有那么充足。指数平滑法就是抓住这个特点,赋予最新的数据较高的权重,而其他数据随着时间的增加,其权重也随之降低。
一般来说,当时间序列数据呈稳定的水平趋势时,选择较小的α值,为0.05到0.2之间;当时间序列数据有波动,但长期趋势变化不大,可选稍大的α值,常在0.1-0.4之间;当时间序列数据波动很大,长期趋势变化幅度较大,是明显且迅速的上升或下降趋势时,宜选择较大的α值,可在0.6-0.8之间,以使模型灵敏度高些,迅速跟上数据的变化;当时间序列数据是上升(或下降)的发展趋势,a应取较大的值,在0.6-1之间。
比如有以下13期的实际需求数据
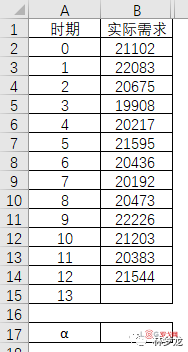
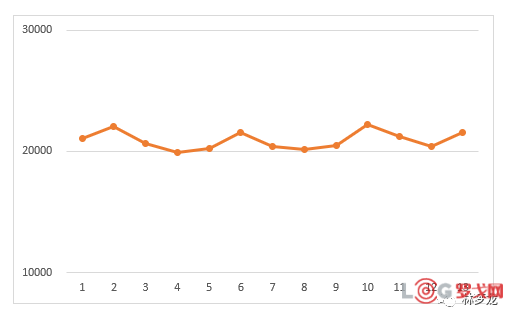
通过图例,实际需求还是比较稳定,因此初始α值选择0.2。而第0期的预测值为21054,通过一次指数平滑公式
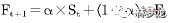


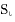

得出结果如下:
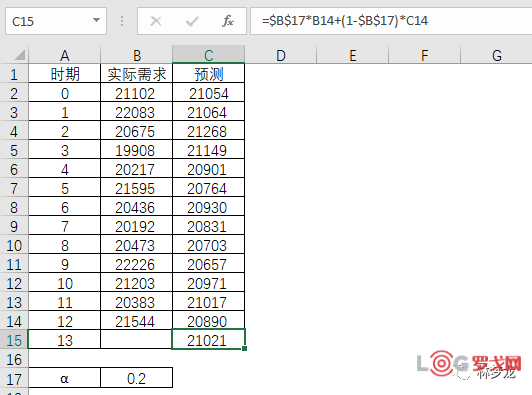
尽管如此,这个0.2的值是否适合了,凭此计算出的预测值21021,是否也值得可信。
一般来说,为了让选择的α值适合,预测和实际之间的MAPE(Mean Absolute Percentage Error, 平均绝对百分比误差)要达到最优化。
因此,0.2的取值计算得出的MAPE为3.25%

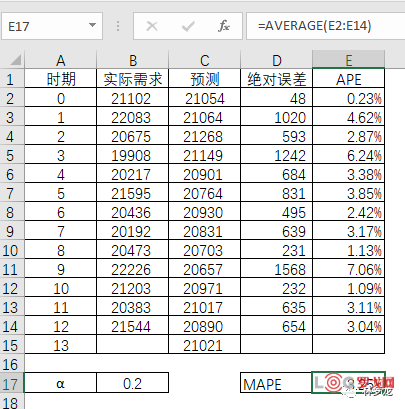
规划求解可以帮忙我们求出适合的α值,让MAPE值最小。
但是规划求解有个缺陷,就是取值只能大于等于0,而指数平滑的α值应为0到1之间,因此规划求解即可取0也可以取值1,就是有点矛盾。当然要解决这个还是有办法的,但是不在本篇讨论中。
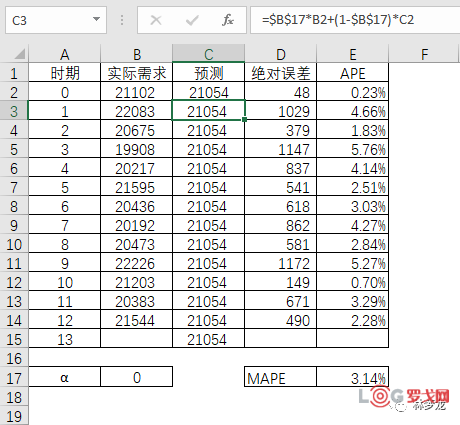
先看一下结果。约束计算下,如果α为0的时候,MAPE最小,为3.14%。这个情况下,下一期的预测值为21054。
不过如果初始期预测值为21706的时候,通过规划求解,可以得出MAPE在α值取值0.4左右的时候,为3.51%
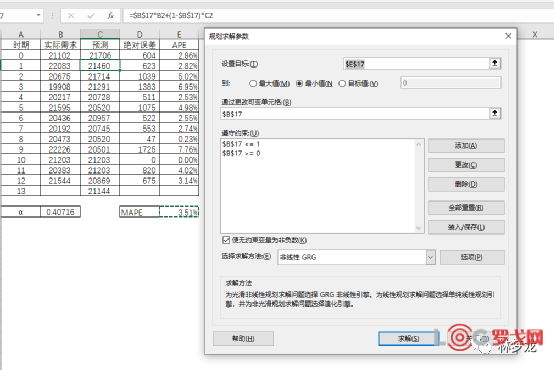
那么,这情况下指数α可以考虑取值0.4来计算。从图例来看,取值0.4也比较符合这个特点:当时间序列数据有波动,但长期趋势变化不大,可选稍大的α值,常在0.1-0.4之间。
这是对指数选择的一个不错的方法。

2024最值钱的物流上市企业是谁?哪些物流企业被看好,哪些被看跌?
1667 阅读
地缘政治重塑下的全球供应链:转型、挑战与新秩序
1340 阅读
物流供应链领域“吸金”不力,但能给投融资事件颁几个奖
1329 阅读连续5年的“春节主力军”,德邦为何如此稳?
1219 阅读扎根供应链创新25年,一家“耐力长跑型”企业的破局启示
991 阅读中远海运回应被美国国防部列入“中国军事企业”清单
1001 阅读CES 2025:NVIDIA OMNIVERSE驱动的智能仓储数字孪生革命
1014 阅读拼多多引领电商西进:帝王蟹进村,非遗剪纸出山
933 阅读制造业企业,不要逼物流公司降价了!
809 阅读满帮旗下山恩保险经纪2024年联合保险公司提供9970亿元货运风险兜底
801 阅读